Ensemble Methods - Decision Trees and Bagging

Week 6 | Lesson 2.3

LEARNING OBJECTIVES

After this lesson, you will be able to:

Explain the power of using ensemble classifiers
Know the difference between a base classifier and an ensemble classifier
Describe how bagging works
Use the bagging classifier in scikit-learn

STUDENT PRE-WORK

Before this lesson, you should already be able to:

Perform a classification
Use label encoder
Use cross validation to evaluate model performance

INSTRUCTOR PREP

Before this lesson, instructors will need to:

Read in / Review any dataset(s) & starter/solution code
Generate a brief slide deck
Prepare any specific materials
Provide students with additional resources

LESSON GUIDE

Opening (10 min)

In the previous lectures we learned about Decision Trees, APIs and SQL Joins: many different techniques that combined together give us powerful tools to analyze and process data. Today we will learn about ensemble techniques: ways to combine different models in order to obtain a more powerful model.

Before we dive into the subject, let's recap a few things learned so far:

Check: What classifiers have we learned about so far? Which one is your favourite?

KNN, Logistic Regression, Decision Trees, Support Vector Machines

Check: How did we assess the "goodness" of a particular model?

Cross validation, various scores...

Check: Any idea on how we could improve the performance of a model?

Mixing more models

Introduction: Ensemble Techniques (30 min)

Ensembles

Ensemble techniques are supervised learning methods to improve predictive accuracy by combining several base models in order to enlarge the space of possible hypothesis to represent our data. Ensembles are often much more accurate than the base classifiers that compose them.

Check: Short discussion:

When this might be useful?
Can you think of a business case where we may want to get a very very accurate model (despite it being more complex)
Answer: for example when lives are at stake or the outcome of an error is very costly:
- medical data models
- failure in airplane engines
- etc.

Two families of ensemble methods are usually distinguished:

In averaging methods, the driving principle is to build several estimators independently and then to average their predictions. On average, the combined estimator is usually better than any of the single base estimator because its variance is reduced.

Examples of this family include Bagging methods and Random Forest.

The other family of ensemble methods are boosting methods, where base estimators are built sequentially and one tries to reduce the bias of the combined estimator. The motivation is to combine several weak models to produce a powerful ensemble. We will discuss these in a future lecture.

Examples of this family include AdaBoost and Gradient Tree Boosting.

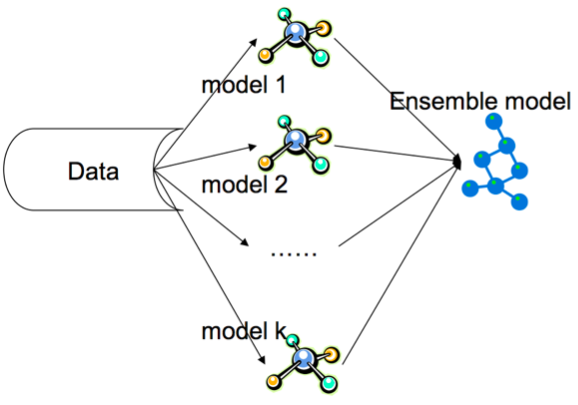
The Hypothesis space

In any supervised learning task, our goal is to make predictions of the true classification function $f$ by learning the classifier $h$. In other words we are searching in a certain hypothesis space for the most appropriate function to describe the relationship between our features and the target.

Check: Can you give an example of how this search is performed using one of the classifiers you know?

Answer: e.g. in logistic regression we have a space of all possible logistic functions. The best hypothesis is found by choosing the value of the parameters that maximize the accuracy of predictions.

Check: What reasons could be preventing our hypothesis to reach perfect score?

Answer: the problems below

There could be several reasons why a base classifier doesn't perform terribly well in trying to approximate the true classification function. These are of three types:

Statistical
Computational
Representational

The Statistical Problem

If the amount of training data available is small, the base classifier will have difficulty converging to $h$.

An ensemble classifier can mitigate this problem by "averaging out" base classifier predictions to improve convergence. This can be pictorially represented as a search in a space where multiple partial perspectives are combined to obtain a better picture of the goal.

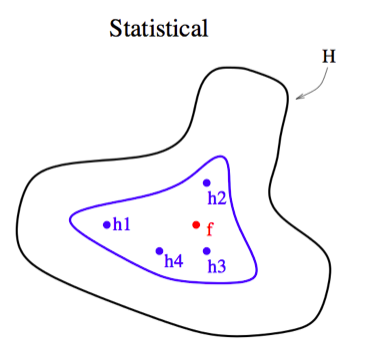
(source: http://www.cs.iastate.edu/~jtian/cs573/Papers/Dietterich-ensemble-00.pdf)

The true function $f$ is best approximated as an average of the base classifiers.

Check: How would you re-phrase the statistical problem?

The Computational Problem

Even with sufficient training data, it may still be computationally difficult to find the best classifier $h$.

For example, if our base classifier is a decision tree, an exhaustive search of the hypothesis space of all possible classifiers is extremely complex (NP-complete).

In fact this is why we used a heuristic algorithm (greedy search).

An ensemble composed of several Base Classifiers’s with different starting points can provide a better approximation to $f$ than any individual Base Classifiers.

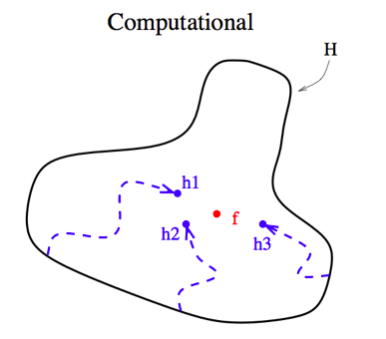
The true function $f$ is often best approximated by using several starting points to explore the hypothesis space.

Check: How would you re-phrase the computational problem?

The Representational Problem

Sometimes $f$ cannot be expressed in terms of our hypothesis at all. To illustrate this, suppose we use a decision tree as our base classifier. A decision tree works by forming a rectilinear partition of the feature space, i.e it always cuts at a fixed value along a feature.

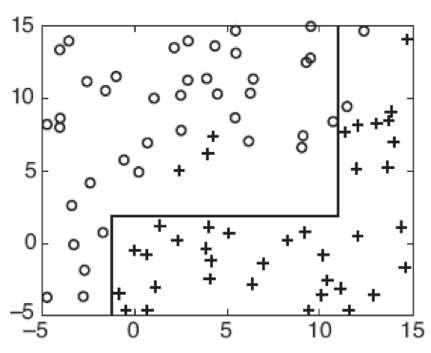
But what if $f$ is a diagonal line?

Then it cannot be represented by finitely many rectilinear segments, and therefore the true decision boundary cannot be obtained by a decision tree classifier.

However, it may be still be possible to approximate $f$ or even to expand the space of representable functions using ensemble methods.

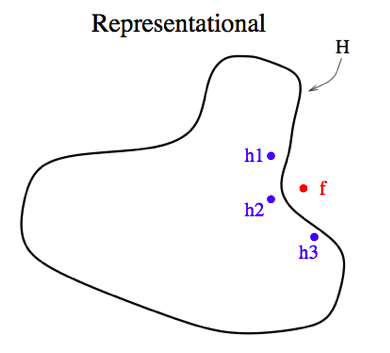
Check: How would you re-phrase the representational problem?

Characteristics of Ensemble methods

In order for an ensemble classifier to outperform a single base classifier, the following conditions must be met:

accuracy: base classifiers outperform random guessing
diversity: misclassifications must occur on different training examples

Check: What base classifiers would you combine to have different perspectives?

Guided Practice: Find real world uses of ensemble methods (20 min)

There are many examples of real-world uses of ensemble methods, the most famous one probably being the Netflix prize.

In small groups of 3-4 people look for one or two real world applications of ensemble methods and then choose your favourite one to report to the class.

Here are some sources to start your search:

Instructor Note: leave 10 minutes for the search and 10 minutes for sharing in class

Introduction: Bagging (10 min)

Bagging or bootstrap aggregating is a method that involves manipulating the training set by resampling. We learn $k$ base classifiers on $k$ different samples of training data. These samples are independently created by resampling the training data using uniform weights (e.g. a uniform sampling distribution). In other words each model in the ensemble votes with equal weight. In order to promote model variance, bagging trains each model in the ensemble using a randomly drawn subset of the training set. As an example, the random forest algorithm combines random decision trees with bagging to achieve very high classification accuracy.

Original	1	2	3	4	5	6	7	8
Training set 1	2	7	8	3	7	6	3	1
Training set 2	7	8	5	6	4	2	7	1
Training set 3	3	6	2	7	5	6	2	2
Training set 4	4	5	1	4	6	4	3	8

Given a standard training set $D$ of size $n$, bagging generates $m$ new training sets $D_i$, each of size $n'$, by sampling from $D$ uniformly and with replacement. By sampling with replacement, some observations may be repeated in each $D_i$. The $m$ models are fitted using the above $m$ samples and combined by averaging the output (for regression) or voting (for classification).

Bagging reduces the variance in our generalization error by aggregating multiple base classifiers together (provided they satisfy our earlier requirements).

If the base classifier is stable then the ensemble error is primarily due to bias, and bagging may not be effective.

Since each sample of training data is equally likely, bagging is not very susceptible to overfitting with noisy data.

As they provide a way to reduce overfitting, bagging methods work best with strong and complex models (e.g., fully developed decision trees), in contrast with boosting methods which usually work best with weak models (e.g., shallow decision trees).

Check: Can you propose another sample to add to those above? Call out the numbers you would include.

Answer: any subsample of 8 numbers with replacement pulled from the set of digits [1,..,8].

Demo: Bagging Classifier in Scikit Learn (15 min)

In scikit-learn, bagging methods are offered as a unified BaggingClassifier meta-estimator (resp. BaggingRegressor), taking as input a user-specified base estimator along with parameters specifying the strategy to draw random subsets. In particular, max_samples and max_features control the size of the subsets (in terms of samples and features), while bootstrap and bootstrap_features control whether samples and features are drawn with or without replacement. When using a subset of the available samples the generalization error can be estimated with the out-of-bag samples by setting oob_score=True.

As an example, we will compare the performance of a simple KNN classifier versus the Bagging Classifier on the car acceptability dataset.

The first step is to load the data into Pandas. Do it on your own:

Import pandas
Load the data from a csv file

Solution:

import pandas as pd
df = pd.read_csv('./assets/datasets/car.csv')

df.head()

	buying	maint	doors	persons	lug_boot	safety	acceptability
0	vhigh	vhigh	2	2	small	low	unacc
1	vhigh	vhigh	2	2	small	med	unacc
2	vhigh	vhigh	2	2	small	high	unacc
3	vhigh	vhigh	2	2	med	low	unacc
4	vhigh	vhigh	2	2	med	med	unacc

Since most of the features are categorical text we will need to encode them as numbers using the LabelEncoder:

from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
features = [c for c in df.columns if c != 'acceptability']
for c in df.columns:
    df[c] = le.fit_transform(df[c])

X = df[features]
y = df['acceptability']

Notice that we overwrote the original features for simplicity, since we are not interested in doing a study on feature importance.

Check: Is it correct to use the label encoder blindly like this?

Answer: no, it's not correct, because the categorical features have a scale. It would be more appropriet to do one of the following:

either use pd.get_dummies to encode them as binaries

use a map that correctly assigns a numerical scale to the values, e.g. where med > small

The next step is to calculate the cross_val_score on the two classifier:

from sklearn.cross_validation import cross_val_score
from sklearn.ensemble import BaggingClassifier
from sklearn.neighbors import KNeighborsClassifier

knn = KNeighborsClassifier()
bagging = BaggingClassifier(knn, max_samples=0.5, max_features=0.5)

print "KNN Score:\t", cross_val_score(knn, X, y, cv=5, n_jobs=-1).mean()
print "Bagging Score:\t", cross_val_score(bagging, X, y, cv=5, n_jobs=-1).mean()

KNN Score:    0.643070305149
Bagging Score:    0.722795402608

Check: Does bagging interfere with grid search? Are we leaking data and thus faking the cross val score?

Answer: We are not leaking data. Bagging acts on the training sample for each fold, so it is not aware of the data in the test fold. You can convince yourself of this by doing a simple train test split

Bagging Classifier details

The BaggingClassifier meta-estimator has several parameters.

Check: In pairs, look at the documentation for a detailed description of each and find out what max_samples and max_features do.

Answer:

max_samples is the number of samples to draw from X to train each base estimator, can be given as absolute number or fraction of the total

max_features is the number of features to draw from X to train each base estimator, can also be given as absolute or fraction.

Independent Practice (10 min)

Take a dataset of your choice and practice comparing the score of a base classifier with the bagging classifier. Explore also the effect of changing one or more parameters.

For example could use one of the dataset of the week5/5.2-lab or any other dataset of your choice.

Conclusion (5 min)

Today we have learned about Ensemble Models and Bagging Classifier. We have learned how they improve the performance of individual base models thanks to their better ability to approximate the real prediction function in a supervised learning problem.

2.3 Ensemble Methods - Decision Trees and Bagging