 Math Primer 2
Math Primer 2
Week 1 | Lesson 4.1
LEARNING OBJECTIVES
After this lesson, you will be able to:
- Describe a matrix and an array
- Explain how to add and subtract arrays
- Explain the dot product
STUDENT PRE-WORK
Before this lesson, you should already be able to:
- [intro to arrays] (https://www.khanacademy.org/computing/computer-programming/programming/arrays/p/intro-to-arrays#)
STARTER CODE
LESSON GUIDE
| TIMING | TYPE | TOPIC |
|---|---|---|
| 5 min | Introduction | Matrices, arrays, the dot product |
| 20 min | Demo / Guided Practice | Matrices and arrays |
| 20 min | Demo / Guided Practice | Adding and subtracting arrays |
| 20 min | Demo / Guided Practice | The dot product |
| 20 min | Independent Practice | |
| 5 min | Conclusion |
Introduction: Why Use arrays? (5 mins)
An array is a collection of related data items, called elements, associated with a single variable name. Arrays can ease programming and offer improved performance. When writing an application, you are usually faced with the problem of storing and manipulating large collections of data. Arrays simplify the task of naming and referencing the individual items in each collection. Using arrays can boost the performance of your application . Arrays let you manipulate an entire collection of data items with a single statement.
Demo / Guided Practice / Demo: Matrices and arrays (20 mins)
An array is a data structure that allows you to group several numeric or string variables under a single name. A vector is a one-dimensional array, a table or a matrix is two-dimensional array, or an array may have several dimensions. An array may contain either string or numeric values, but a given array may not contain both types of values.
As mentioned above, a matrix is a specific type of array, that is 2D.
Here's a great picture showing the difference between vectors, matrices, and arrays.
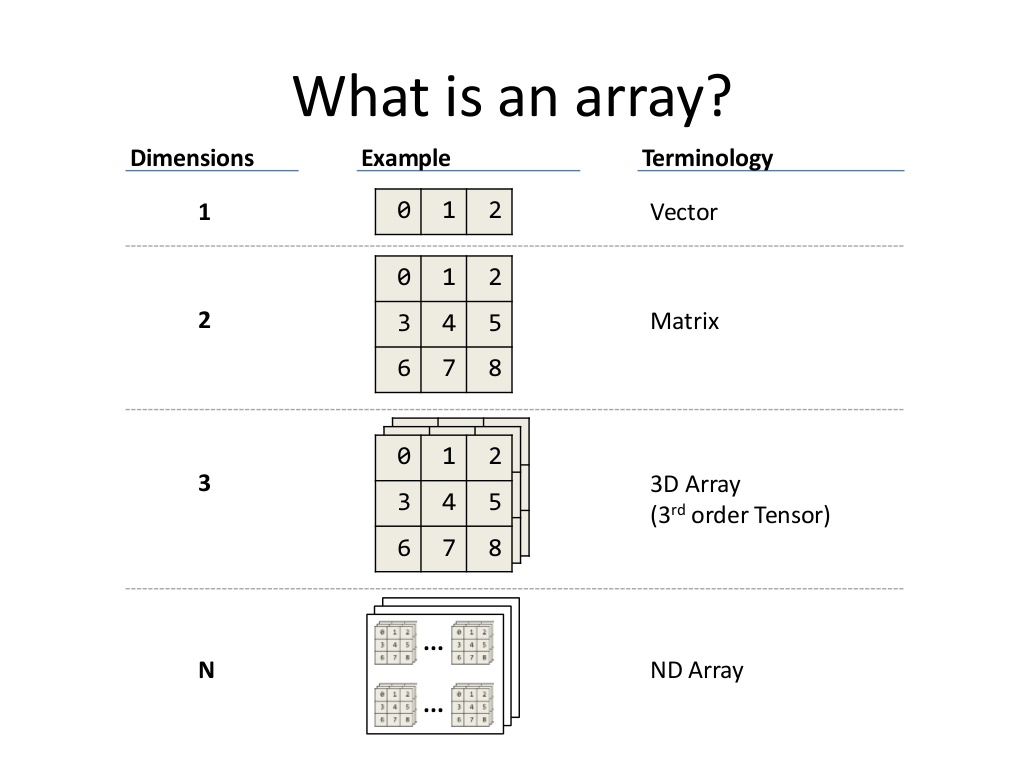
Here is some information on vectors, matrices, arrays.
Let's use the following demo code to get started.
First, use numpy to create an array.
in Jupyter notebook type:
import numpy as np
a = np.array([1, 2, 3, 4, 5])
b = np.array([5, 4, 3, 2, 1])
You've just created your first two arrays! Since we know that matrices are simply a 2D array, we'll just keep keep our focus on arrays for the moment. Since there may be some confusion using matrices and arrays, some Python users find it easier just to stick with arrays.
You can read more about the confusion between the two and some problems that arise here
Check What is the difference between a vector, a matrix, and an array? Is a vector an array? Is an array a vector? Is a matrix an array? Is an array a matrix? Can arrays have both numeric and string values?
Demo / Guided Practice / Demo: Adding and subtracting two arrays (20 mins)
Let's take a look at the two arrays we just created above.
a = [1, 2, 3, 4, 5]
b = [5, 4, 3, 2, 1]
Let's add them together. [6, 6, 6, 6, 6]
Now, let's let numpy do the work. in Jupyter notebook type:
np.add(a, b)
Thanks numpy, that was easy!
Let's try subtraction. [-4, -2, 0, 2, 4]
Now, let's let numpy do the work. in iPython notebook type:
np.subtract(a, b)
Thanks numpy, that was easy!
Demo / Guided Practice / Demo: The dot product (20 mins)
The dot product is one way to multiply arrays. The dot product is represented like [this]:
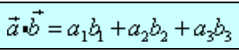
Let's take a look again at the two arrays we just created above:
a = [1, 2, 3, 4, 5]
b = [5, 4, 3, 2, 1]
Using the formula for the dot product that we just learned, let's find the dot product for our two arrays.
1 5 = 5 2 4 = 8 3 3 = 9 4 2 = 8
5 * 1 = 5
35
Now, let's let numpy do the work. in iPython notebook type:
np.dot(a, b)
Thanks numpy, that was easy!
Independent Practice: Topic (20 minutes)
- Create 2 arrays. Add them together, subtract them, and find their dot product.
Conclusion (5 mins)
- What's the difference between a matrix and an array?
- Explain how to add to arrays together, subtract them, get the dot product to a partner.