Merge Sort
Merge Sort
LEARNING OBJECTIVES
After this lesson, you will be able to:
- Explain and implement Merge Sort
STUDENT PRE-WORK
Before this lesson, you should already be able to:
- Explain and implement Bubble and Insertion Sorts
INSTRUCTOR PREP
Before this lesson, instructors will need to:
- Gather blank pieces of paper (1 per student) for use in the demo
- Write random numbers on the paper in a thick marker so it's easily visible
Opening (5 mins)
Instructor Note: Ask students to close their laptops.
While Bubble Sort and Insertion Sort are good for lists and arrays that are already mostly sorted, most data does not arrive that way. For that reason, we need more powerful algorithms. One such algorithm is Merge Sort.
Introduction: Merge Sort (15 mins)
Check: What was a downside to sorting using bubble and insert sort? We had to keep looping through the entire array.
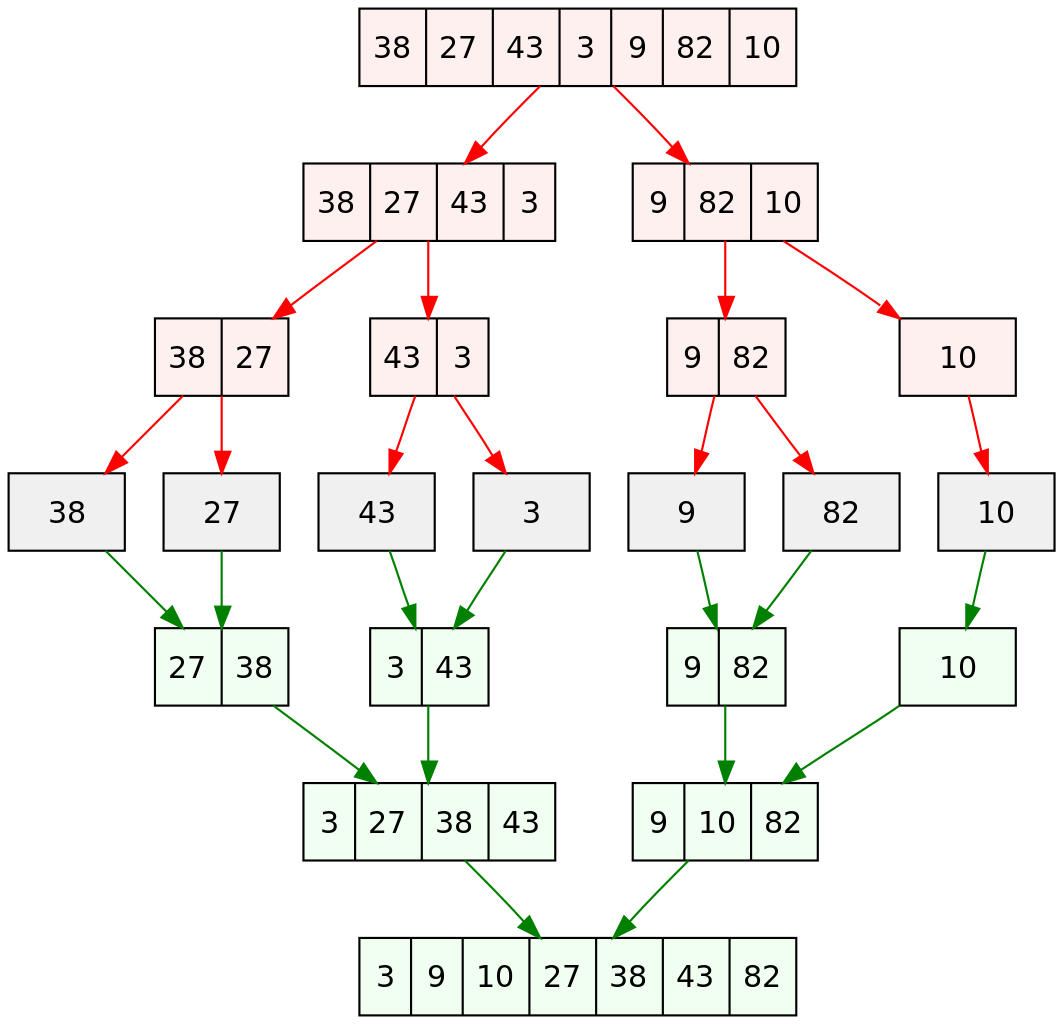
Merge Sort is a "Divide and Conquer" algorithm. Here are the steps:
- A list or array of size n is turned into n sublists with 1 element each.
- Each sublist is sorted.
- Then, the algorithm repeatedly merges sublists together into new, sorted sublists.
- When merging the lists, elements from each list are compared against each other and are added into the merged sublist from smallest to largest.
- This process continues until only the sorted list remains.
You can break the entire process down into two parts.
- Divide the array repeatedly until there are arrays of size 1
- Merge the arrays, sorting as you go.
You can see from those two parts, where the name and type of sort comes from.
Instructor Note: Using the paragraph above, write up the steps for the merge sort and merge methods on the board in an ordered list. You will use this list later.
Check: Discuss this question in pairs: why might a "divide and conquer" algorithm work more quickly than a quadratic algorithm? Have students share out.
Check: How many "levels" did the completed diagram have?
Demo: MergeSort (10 mins)
Instructor Note: On the computer, use a program such as Slides that will allow you to write out numbers and drag them around to re-sort.
Now we are going to walk through an example together on the screen.
Remember that the entire process is split into two primary parts:
- Divide the array repeatedly until there are arrays of size 1
- Merge the arrays, sorting as you go.
Check: Prompt the students for each step.
Demo: MergeSort the students! (10 mins)
Instructor Note: Distribute the randomly numbered pieces of paper, one to each student.
Now, it's time to try the Merge Sort yourselves (literally)! Using the numbers you have, we're going to randomly sort and merge each other!
Instructor Note: Direct the students to perform merge sort using the steps in the ordered list you've written on the board. Facilitate each step.
Guided Practice: Practicing Merge Sort (15 mins)
Work with a partner, and draw out the steps to sort the follow list of numbers: {51, 27, 16, 1, 4, 43, 18, 43, 2, 24, 36, 17, 16, 18, 7, 36, 54, 15, 29, 57, 0}
Check: With 2 minutes left, review a student answer with the class.
Independent Practice: The Merge Sort Algorithm (15 mins)
Use the steps on the board, and your practice sorting as guides to write out the pseudocode for the merge sort.
Hint: The most common solution for this is to split the process into two methods, one to handle splitting the arrays up, and another to handle merging the arrays back together. Refer to the solution below if you get stuck.
Instructor Note: Give students 8 minutes to do this and then review.
Let's review your solutions before you do this in Java:
func mergeSort( var a as array )
if ( n == 1 ) return a
var l1 as array = a[0] ... a[n/2]
var l2 as array = a[n/2+1] ... a[n]
l1 = mergesort( l1 )
l2 = mergesort( l2 )
return merge( l1, l2 )
end func
func merge( var a as array, var b as array )
var c as array
while ( a and b have elements )
if ( a[0] > b[0] )
add b[0] to the end of c
remove b[0] from b
else
add a[0] to the end of c
remove a[0] from a
while ( a has elements )
add a[0] to the end of c
remove a[0] from a
while ( b has elements )
add b[0] to the end of c
remove b[0] from b
return c
end func
Independent Practice: Implementing Merge Sort (25 mins)
Your turn! Using the starter code, and your pseudocode, implement Merge Sort - create the mergeSort method first, then the merge method.
Instructor Note: Have the students work on the mergeSort method for 8 minutes, share the solution, then give them 15 minutes to write the merge method.
Check: Were students able to successfully complete the task? Review one student solution with the class.
Conclusion (5 mins)
As stated before, there is no perfect sorting algorithm. While Insertion Sort is great for shorter, mostly ordered lists, it would be a poor choice to sort larger datasets, such as all entries in a phone book. Similarly, Merge Sort would be unnecessary and inefficient for a list of 20 numbers that are already mostly in the right order.
It would also be great if there was some mathematical notation to compare these algorithms, right? Fortunately for us, there is Big O Notation - we'll be talking about that soon.